70以上 ベクトル 体積 計算 342130-ベクトル 体積 計算
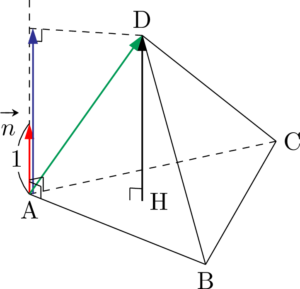
四面体の体積公式 ベクトル利用 を見つけました 高校数学と線形代数 ふくま 数学 とぽろじい 大人の数学自由研究 Note
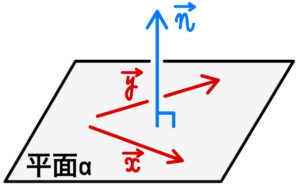
ベクトル場 →A3 = (10x, 10y, 0) の円筒面 S3 ： x2 y2 = 1, − 2 ≤ z ≤ 2 上での面積分を求めよ。 ただし、面素ベクトルの向きは円筒面に対して外向きとする。 解説 まず面 S3 上の位 こんにちは、ウチダです。 今日は数学b「ベクトル」の発展的内容 「(ベクトルの)外積」 について、まずは定義やその意味から解説し、次に具体的な計算方法、そして外積の応用例や
ベクトル 体積 計算
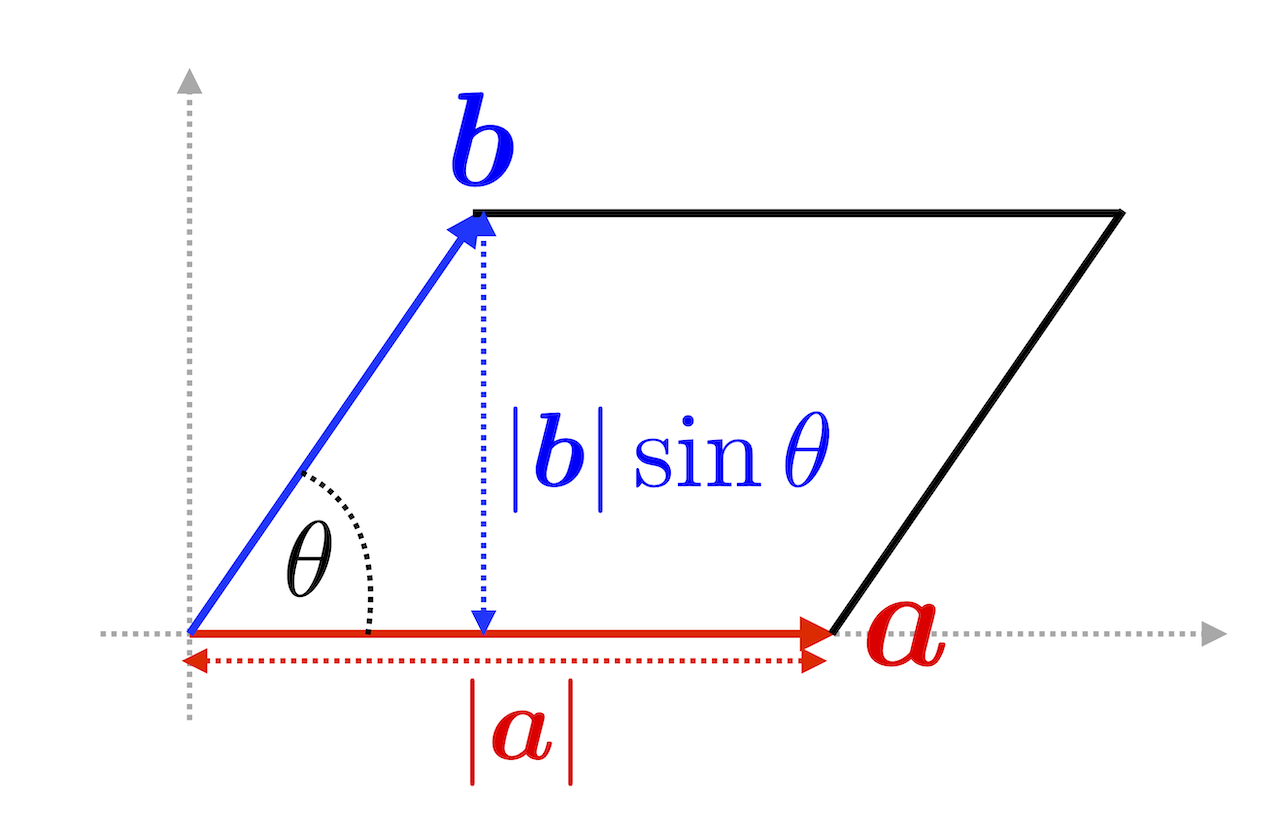
ベクトル 体積 計算-ベクトルにはスカラー積とベクトル積がある 2つの線形独立な任意のベクトル a a と b b に対して、積を考えるとき、次の2つの積があります。 内積と外積 内積（スカラー積）：a ⋅b a ⋅ b 外積（ベク2つのベクトル間の内積、外積を求めます。 = ∑ = × × 1 2⎠ 1 2 2 3 3 2 3 1 1 3 1 2 1 × × × − − − (各ベクトルの下段をクリックして入力) ベクトルの積 product ベクトルの内積abは、aとbが同じ次
大学入試難問 数学解答 数学 数列の和 富岡市の総合学習塾 トータルアカデミー
行列やベクトル（縦ベクトル、横ベクトル）同士の積を計算したときの結果がスカラーなのか、ベクトルなのか、行列なのかをきちんと理解するために、基本的な公式を整理しました。 A x → 、 x1 ベクトルの内積 2つのベクトル に対して，ベクトルの内積（スカラー積，ドット積とも呼ばれる） は，次のように定義される． 例えば，上の例21では，2次元×2の合計4個の成分 からできる ベクトルの内積がかかわる計算問題にチャレンジしてみましょう。 計算問題①「2 つのベクトルがなす角度を求める」 計算問題① つのベクトル , のなす角 を求めよ。 ただし、 とす
21年1月4日 21年11月17日 ベクトルと行列の積は、簡単に言うと「ベクトルを行列に入力して新たなベクトルを出力すること」です。 これは、線形代数のさまざまな概念を理解す ベクトルの外積は この外積の定義を覚えてください というのは簡単ですがおすすめの覚え方があるので紹介しておきます 外積計算のポイントは 求めたい行以外のたすき掛け です どそれとベクトルaとの内積はスカラーになるからである．そのため，スカラー3重積と 呼ばれる． スカラー3重積a (b c)は，括弧を省いて，a b cと書かれることもある．この 場合でも，ベクトル積b c
ベクトル 体積 計算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | 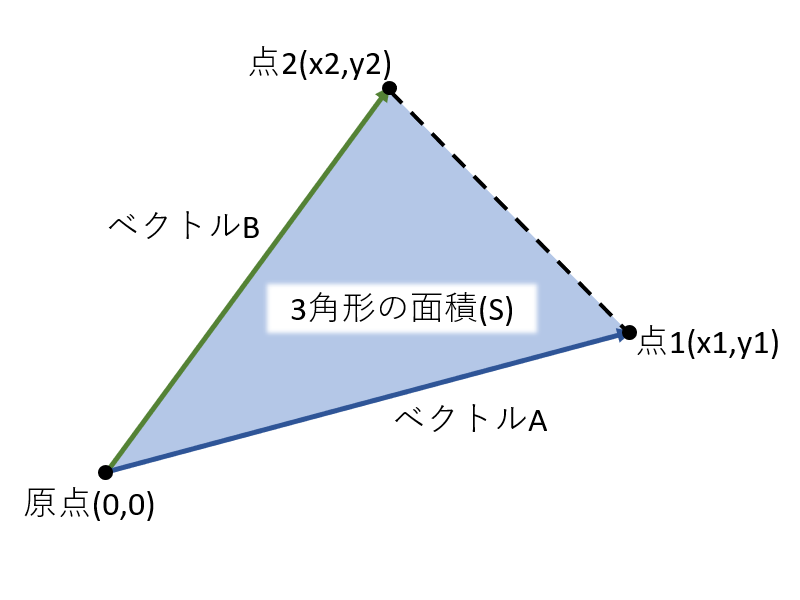 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | 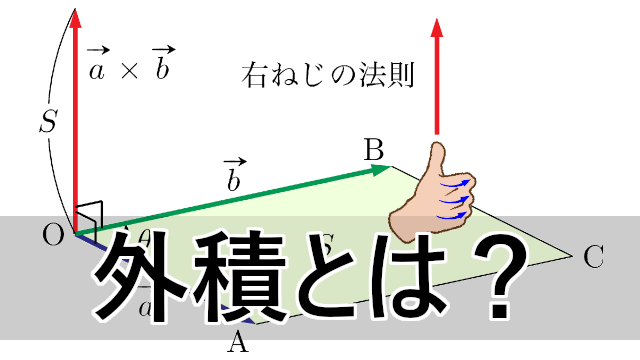 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | 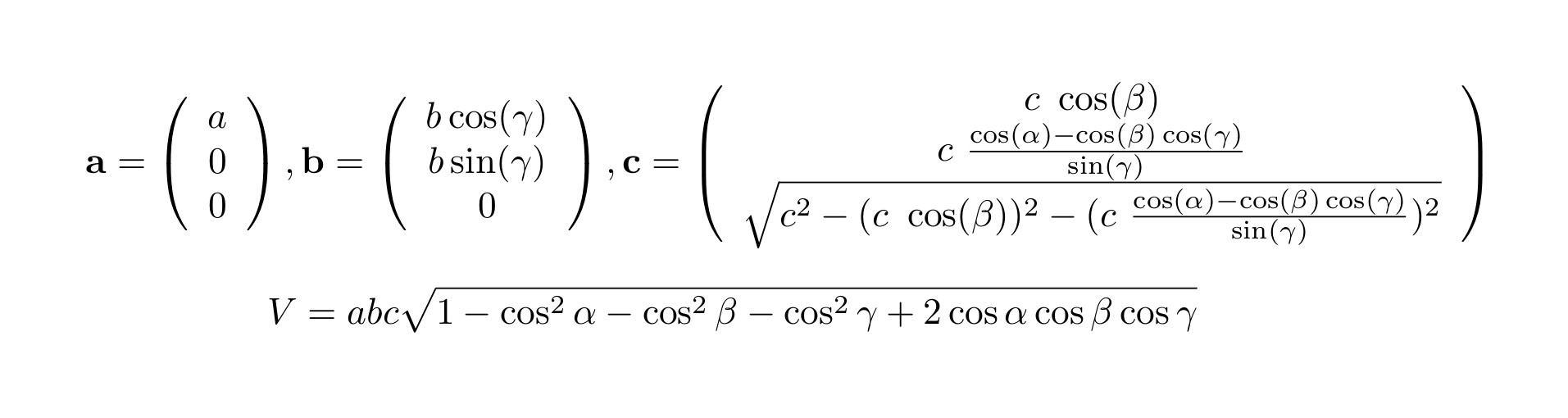 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | 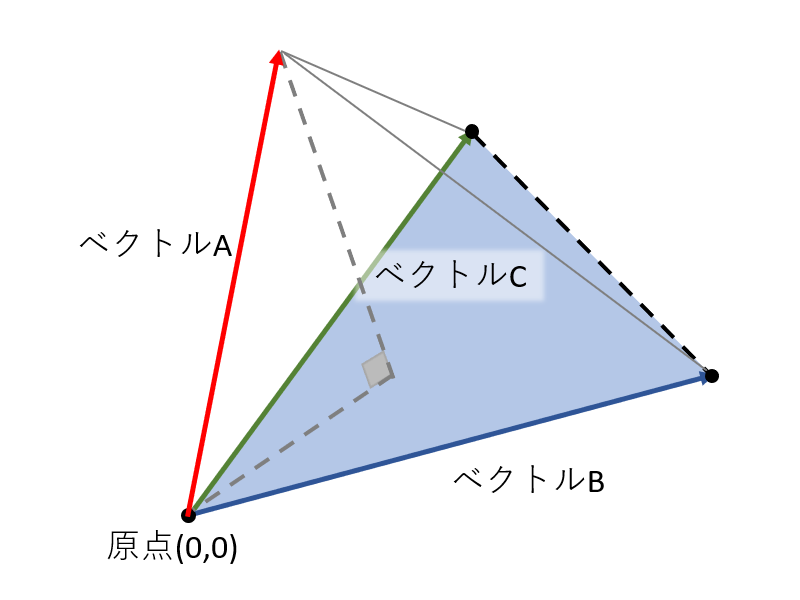 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | 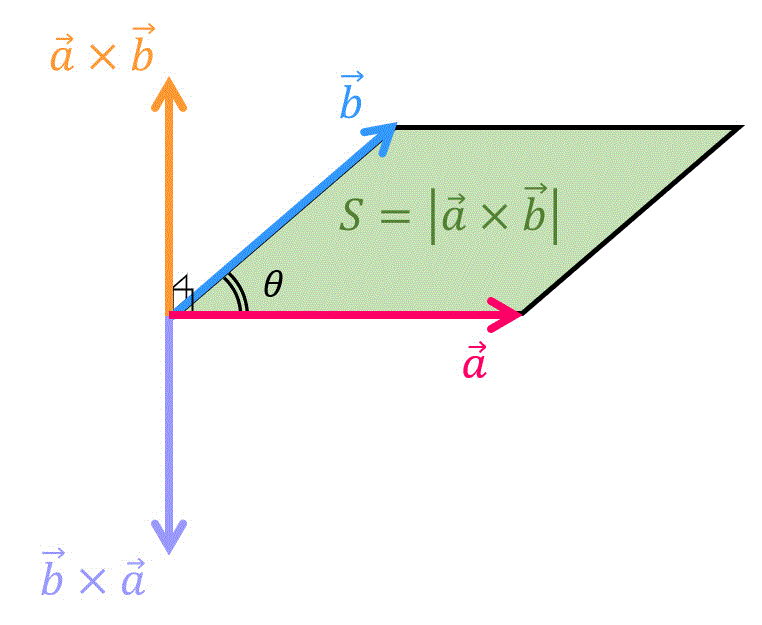 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | 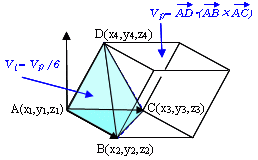 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |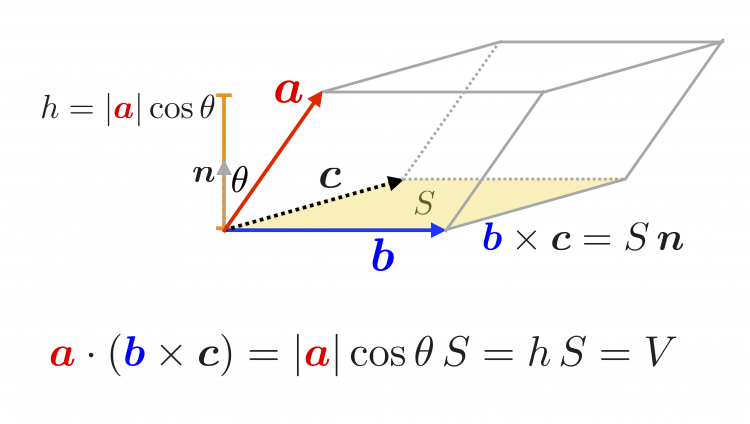
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 | 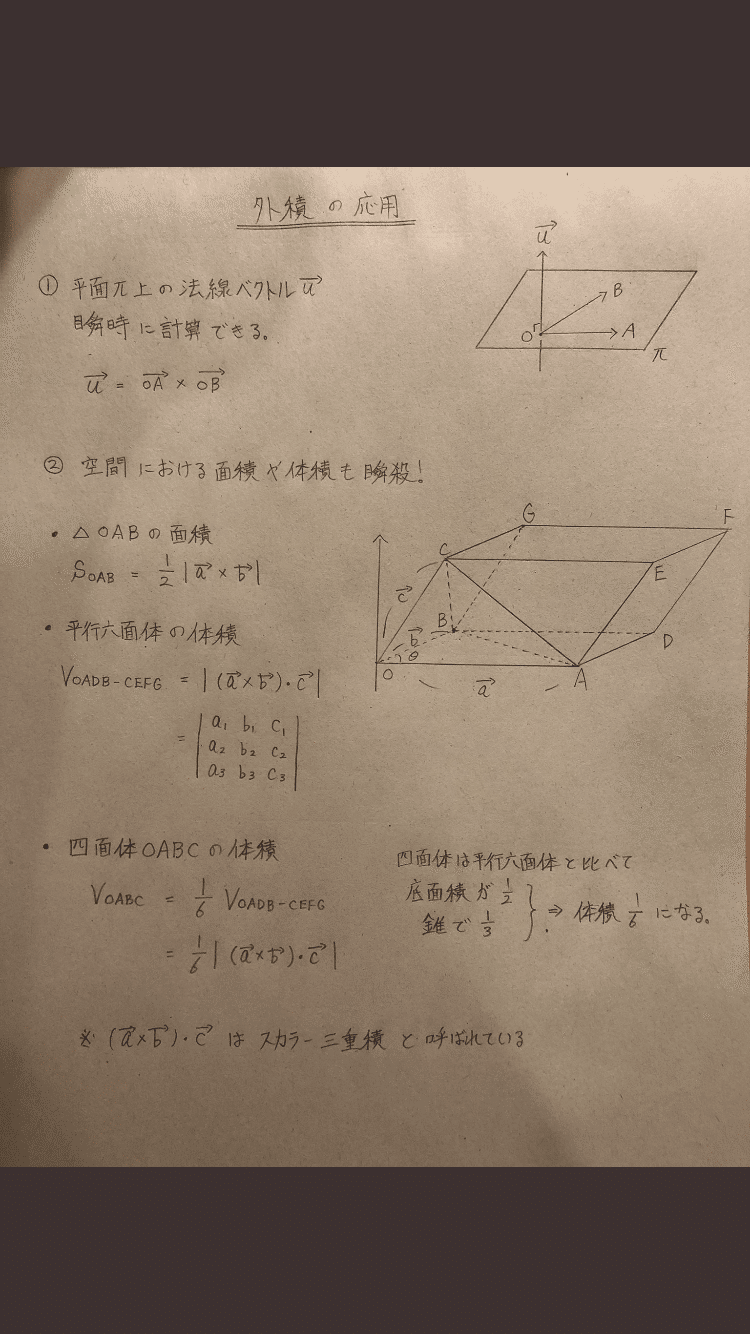 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
 なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |  なぜ行列式を学ぶ 面積 体積との一致 ヤコビアンへの応用 趣味の大学数学 |
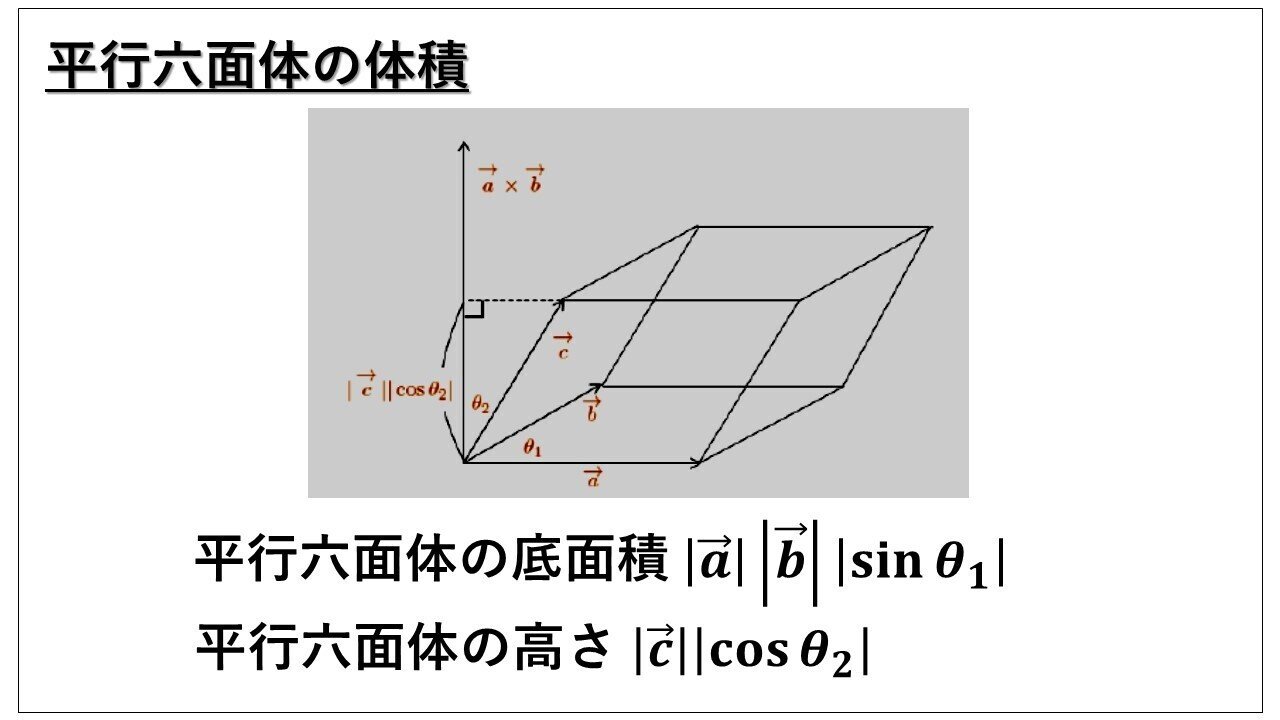
「底面積 × 高さ」が平行六面体の体積です。「ベクトルaとベクトルbの外積」と図のベクトルcで内積をとった値の絶対値が、この「底面積 × 高さ」と一致することを次のように確か ベクトル三重積は、3つのベクトル A, B, C について以下のように定義され、右辺の公式が成り立ちます。 (1) A × ( B × C) = ( A ⋅ C) B − ( A ⋅ B) C 公式1の証明 例題 例題1 A = ( 1, 0, 1),
Incoming Term: ベクトル 体積 計算,
コメント
コメントを投稿